Analog Circuits Custom Design

Category: Analog Circuits

Design Embedded DRAM in Conventional Digital CMOS Process

If an embedded DRAM (eDRAM) block is to be integrated into a System-on-Chip (SoC), a fundamental trade-off arises between cell density and data retention time. Identifying the optimal balance between these two parameters is essential for achieving the desired performance, area efficiency, and reliability. In the following article, this trade-off is analyzed and discussed in detail.

P1 Download

December 2, 2025
Getting Started with Open-Source CMOS Analog IC Design Toolchain
To begin working with open-source tools for CMOS analog IC design, all you need is a computer and a stable internet connection.

It is recommended to install Linux, as all of the essential tools run smoothly on Linux-based systems. Linux distributions are free, and if you are using Windows, you can easily set up a Linux environment through WSL (Windows Subsystem for Linux). For example, I am using Ubuntu on WSL.

Below are the main tools used in a typical analog IC design flow:
- Schematic Capture:
  xschem — https://xschem.sourceforge.io/stefan/index.html
- Circuit Simulation:
  ngspice — https://ngspice.sourceforge.io
- Layout Editor:
  Magic VLSI — http://opencircuitdesign.com/magic/index.html
- Open PDK:
  SkyWater SKY130 — http://opencircuitdesign.com/open_pdks/index.html
Integrating Xschem with SKY130

There are clear instructions available for setting up xschem with the SKY130 PDK:

Documentation:
XSCHEM SKY130 INTEGRATION

A detailed video tutorial is also available, covering xschem, ngspice, and SKY130 PDK usage from scratch:
https://youtu.be/bYbkz8FXnsQ?si=K5OG5g5v23BnFscz
November 16, 2025
MOSFET Small-Signal Characteristics
In this article, we extract the small-signal characteristics of MOSFETs using open-source and free available PDKs and CAD tools. The analysis is carried out using the SkyWater sky130 PDK, Xschem as the schematic capture tool, and Ngspice as the circuit simulator.

All tools (Xschem, Ngfspice, and sky130 PDK) must be installed properly on a Linux system. In this work, Ubuntu running under WSL is used. The installation procedure is discussed in a separate article.

The reader is assumed to have a basic understanding of MOSFET device physics and the fundamentals of MOSFET operation. Figure 1 illustrates the structure and symbols of NMOS and PMOS devices. In integrated-circuit design, each MOSFET has four terminals: gate (G), source (S), drain (D), and bulk (B). Modern CMOS technologies typically employ a p-type substrate; therefore, the bulk of all NMOS devices (except native devices) is tied to the substrate, i.e., GND or VSS. In contrast, PMOS devices are fabricated in isolated wells, allowing their bulks to be biased independently.

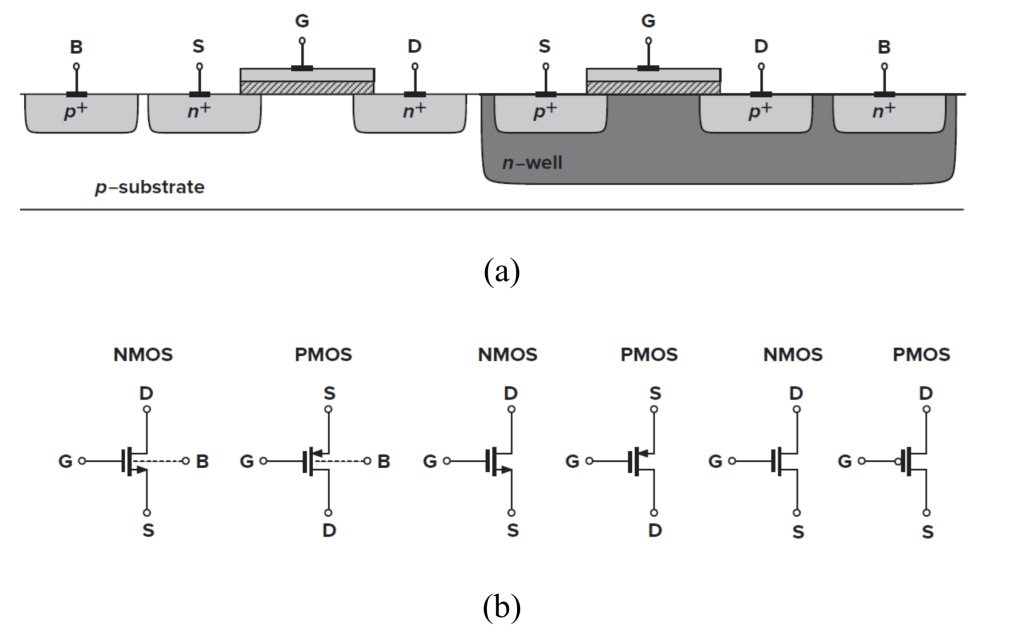
Figure 1: (a) structure of NMOS and PMOS, (b) symbols (from [1])

Operation regions:

A MOSFET behaves as a switch (ON or OFF) in digital design, but in analog design it operates in one of three regions:
- Cut-off (OFF): V_GS < V_TH and V_GD < 0
- Saturation: V_GS > V_TH and V_GD < V_TH
- Triode (ON): V_GS > V_TH and V_GD > V_TH
Note that the transition between these regions is smooth, especially near the threshold voltage.

Voltage – Current Characteristics:

To explain MOSFET operation, we review the V–I equations of an NMOS transistor. PMOS equations follow the same form.

Triode region (ON):

$I_D=\mu_nC_{ox}\frac{W}{L}\left[\left(V_{GS}-V_{TH}\right)V_{DS}-\frac{1}{2}V_{DS}^2\right] \qquad (1)$

For V_DS << 2(V_GS – V_TH):

$I_D\approx\mu_nC_{ox}\frac{W}{L}\left(V_{GS}-V_{TH}\right)V_{DS} \qquad (2)$

Saturation region:

Including channel length modulation,

$I_D=\frac{1}{2}\mu_nC_{ox}\frac{W}{L}\left(V_{GS}-V_{TH}\right)^2(1+\lambda\ V_{DS}) \qquad (3)$

The parameter λ is the channel-length modulation coefficient, which decreases with increasing channel length:

$\lambda\propto\frac{1}{L} \qquad (4)$

Second-order effects:

Body effect: Increasing the source-to-bulk voltage raises the threshold voltage:

$V_{TH}=V_{TH0}+\gamma\left(\sqrt{2\Phi_F+V_{SB}}-\sqrt{\left|2\Phi_F\right|}\right) \qquad (5)$

$\gamma=\frac{\sqrt{2q\epsilon_{si}N_{sub}}}{C_{ox}}\approx0.3\ to\ 0.4\ \left(V^\frac{1}{2}\right) \qquad (6)$

$V_{TH0}=\Phi_{MS}+2\Phi_F+\frac{Q_{dep}}{C_{ox}}=V_{TH}\ for\ V_{SB}=0 \qquad (7)$

Subthreshold (Weak Inversion) : When V_GS ≈ V_TH, the device enters weak inversion, and the drain current follows:

$I_D=I_0\exp{\frac{V_{GS}}{\xi V_T}} \qquad (8)$

where I₀ is proportional to W/L, and ξ > 1 and V_T = kT/q. We say the device operates in weak inversion in contrast with strong inversion.

Small-signal model:

Fig.2 shows the small-signal MOSFET model [1].

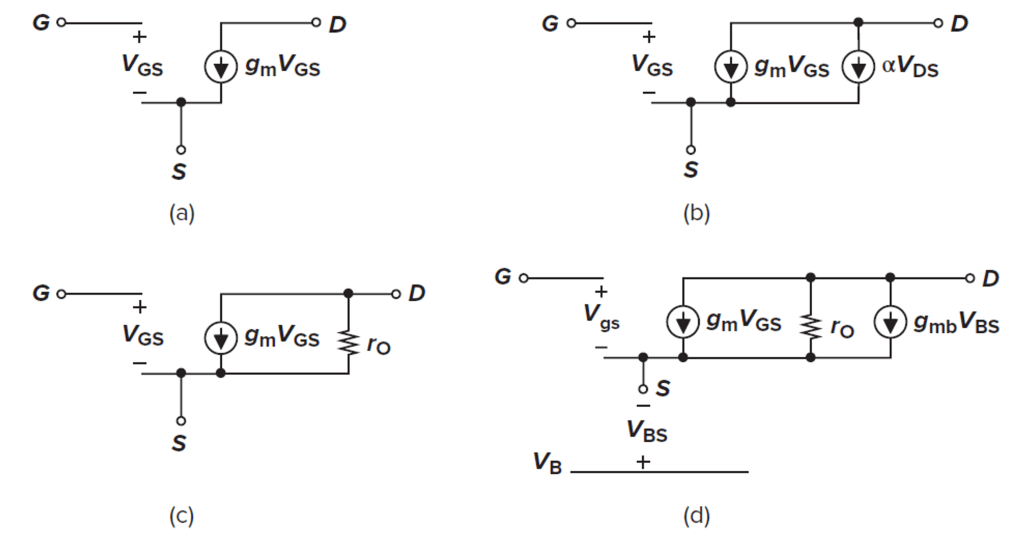
Figure 2: (a) Basic MOS small-signal model; (b) channel-length modulation represented by a dependent current source; (c) channel-length modulation represented by a resistor; (d) body effect represented by a dependent current source. [1]

Equations:

In triode region, a MOSFET behaves as a voltage-controlled resistor:

$R_{on}=\frac{1}{\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH})} \qquad (9)$

In saturation, the transconductance is:

$g_m=\frac{\partial I_D}{\partial V_{GS}} \qquad (10)$

Equivalent expressions include:

$g_m=\mu_nC_{ox}\frac{W}{L}(V_{GS}-V_{TH}) \qquad (11)$

$g_m=\sqrt{2\mu_nC_{ox}\frac{W}{L}I_D} \qquad (12)$

$g_m=\frac{2I_D}{V_{GS}-V_{TH}} \qquad (13)$

The output resistance due to channel-length modulation is:

$r_o=\frac{1}{g_{ds}}=\frac{\partial V_{DS}}{\partial I_D}=\frac{1}{\frac{1}{2}\mu_nC_{ox}\frac{W}{L}\left(V_{GS}-V_{TH}\right)^2\times\lambda} \qquad (14)$

For λV_DS << 1,

$r_o=\frac{1}{g_{ds}}\approx\frac{1+\lambda V_{DS}}{\lambda I_D}\approx\frac{1}{\lambda I_D} \qquad (15)$

The body-effect transconductance is:

$g_{mb}=\frac{\partial I_D}{\partial V_{BS}}=gm\frac{\gamma}{2\sqrt{2\Phi_F+V_{SB}}}=\eta\ g_m \qquad (16)$

where η is typically around 0.25

Simulation results:

Long-channel NMOS: The circuit in fig. 3 is used to evaluate the small-signal, low frequency behavior of an NMOS device. Because capacitances are not considered in this section, DC-sweep analysis is employed.

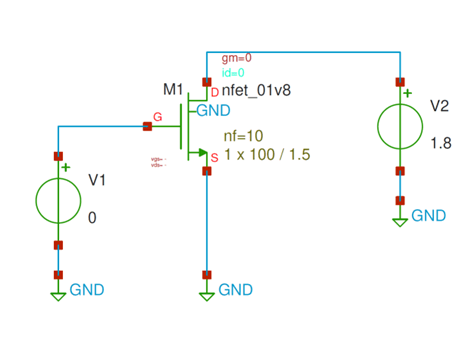
Figure 3: Simple NMOS circuit used for DC-sweep analysis

Here, the W/L is 100u/1.5u, number of gates (fingers) are 10, and the V_GS sweep is from 0 to 1.8V. Fig. 4 shows g_m and g_ds of the NMOS versus V_GS.

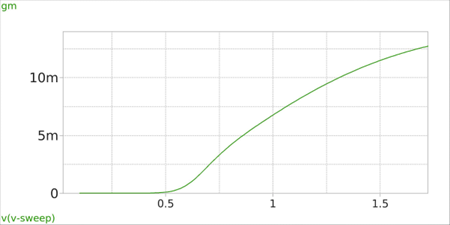
Figure 4(a)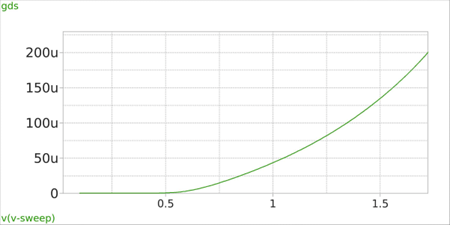

Figure 4(b)

In this circuit, V_TH ≈ 560mv. As expected, by increasing V_GS, both g_m and g_ds increase. It’s interesting to see the g_ds– I_D relationship as shown in fig. 5. The curve is nearly linear, and according to (15), its slope is corresponds to the channel-length modulation coefficient λ.

Figure 5: g_ds vs. I_D

The intrinsic small-signal gain of a MOSFET is defined as

$A_v=g_mr_o=\frac{g_m}{g_{ds}} \qquad (17)$

Fig. 6 plots the gain vs. V_GS.

Figure 6: Intrinsic small-signal low-frequency gain of NMOS with W/L = 100u/1.5u

In this example of long-channel NMOS, the gain peaks at an overdrive voltage of V_ov = V_GS – V_TH ≈ 100 mV.

As V_ov (and thus I_D) increases, the gain decreases. Below V_ov ≈ 80 mV, the device is in weak inversion, and for V_GS < V_TH, the gain loses its physical meaning.

Short-channel (sub-micron) NMOS: For channel length below 1 um (sub-micron), the MOS device behavior is significantly affected by short-channel and higher-order effects. Figure 7 illustrates how these phenomena alter the small-signal parameters for a device with W/L = 10u/0.15u. Detailed discussion of short-channel devices will be provided in a subsequent article.

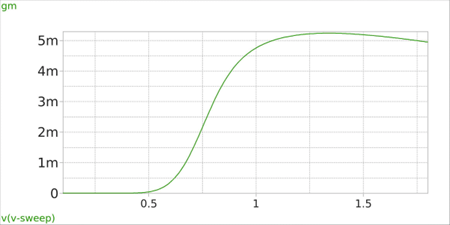
Figure 7(a)

Figure 7(b)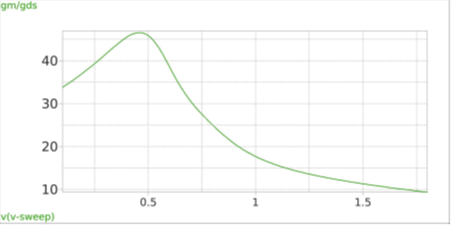

Figure 7(c)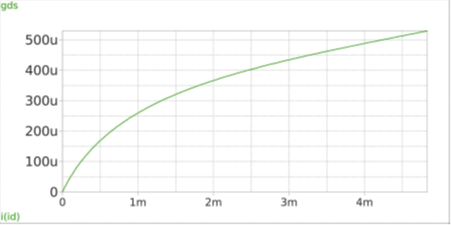

Figure 7(d)

[1] Razavi, B., Design of Analog CMOS Integrated Circuits, 2nd ed. New York, NY, USA: McGraw-Hill, 2017.
November 15, 2025